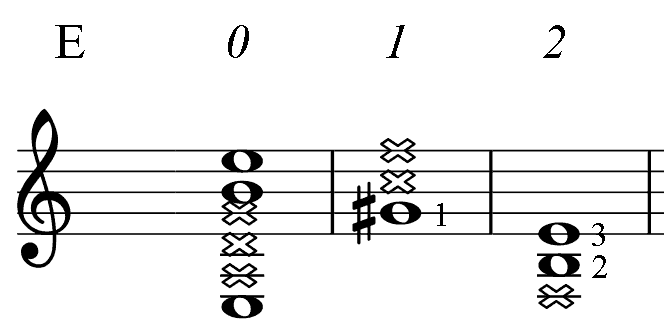
Home | Top | What is PAD: Perfectly Aligning Diagrams | How the method was developed | Basic chord fingering chart | Table of PADs in the Book: chords and scales, transposition table | Musical structure of guitar starting with C major scale | Essential guitar scale pattern on the fretboard | Notes along the fingerboard: note C | Grouping of notes across the guitar strings into fret groups | Notes along the strings | Thirds intervals on the Guitar. Exercise | Guitar Triads and Tetrads (Chords), Diagonal Structure, Exercise | Chords and Inverted Chords on a Guitar Fret Group. Exercise | PAD Chord Charts | Working with other keys, C blues scale and A minor scale and key | Importance of Key Signatures | Guitar Ear, Fingering, Memory Training with Visual Musical Notes Presentation | The book | Success without memorizing | Blogs, Forums, Groups
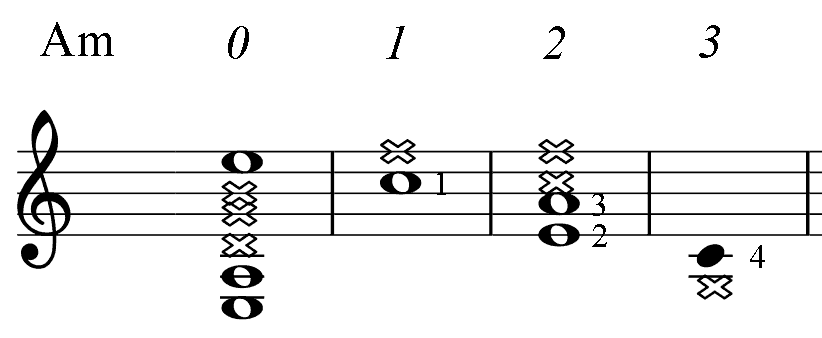
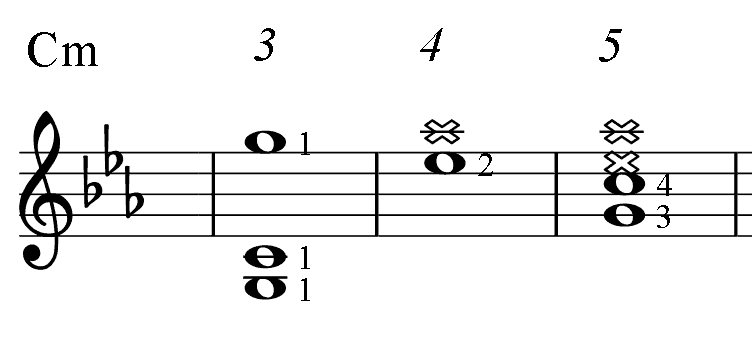
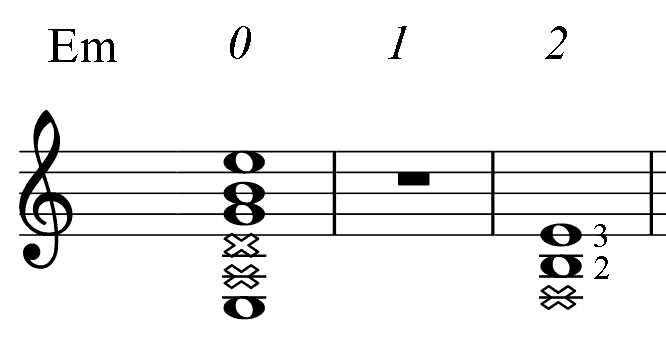
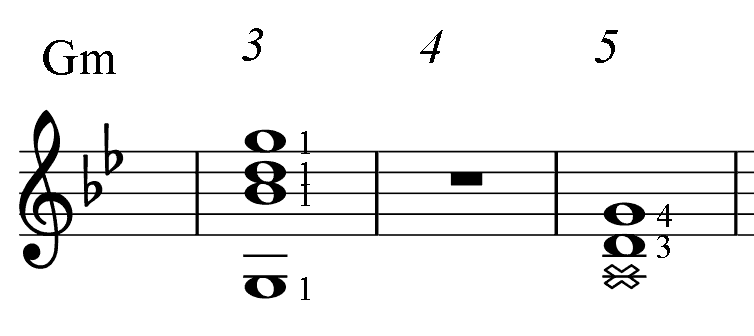
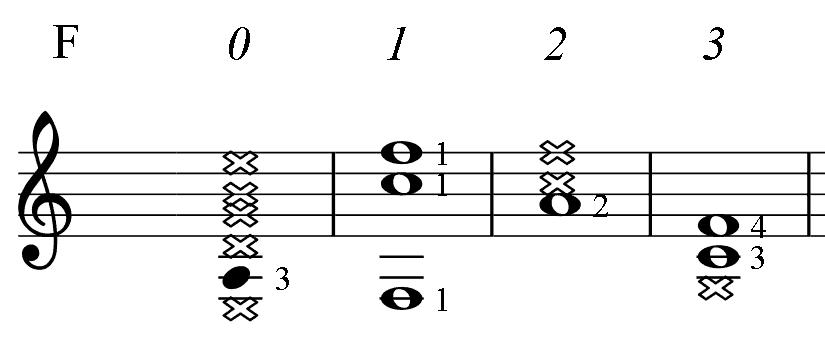
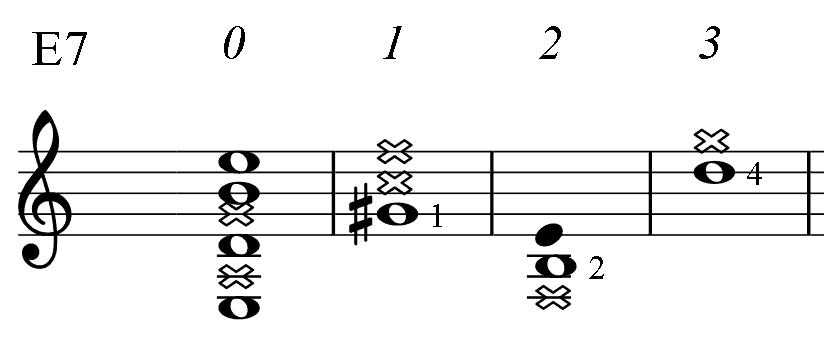
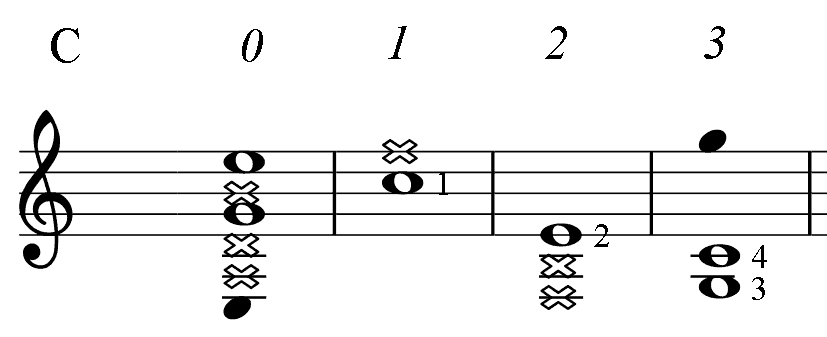
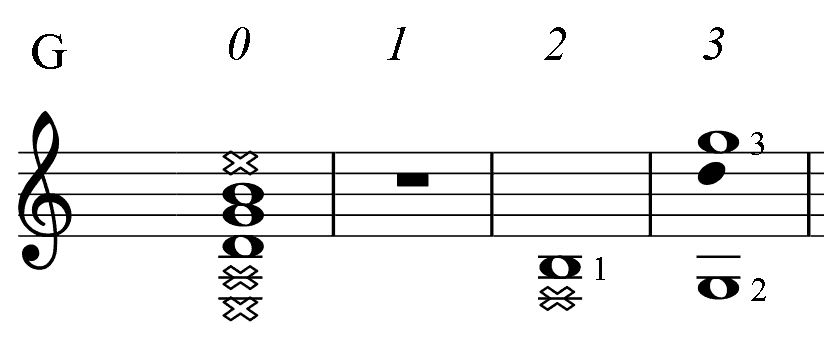
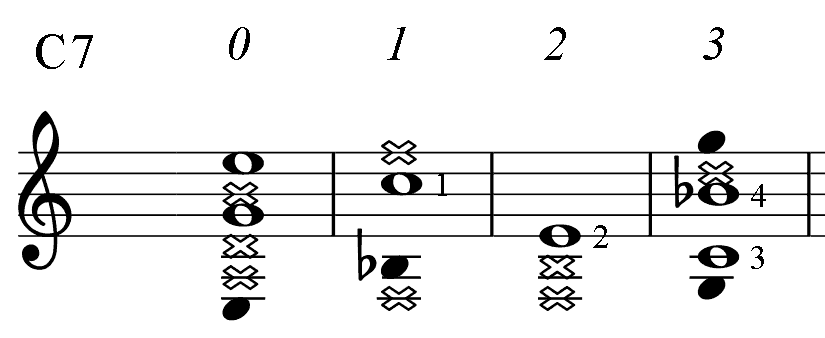
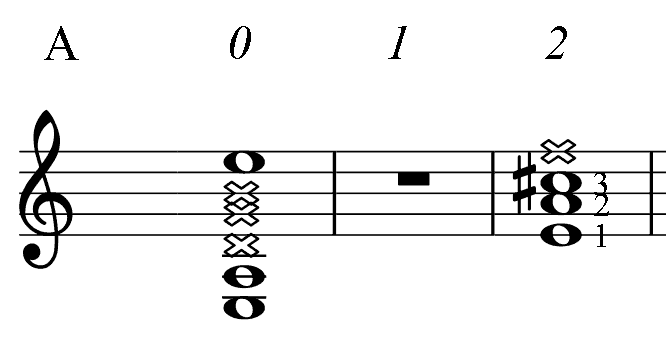
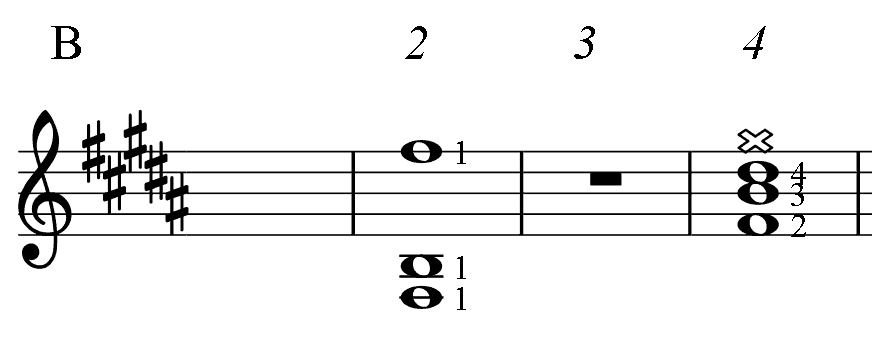
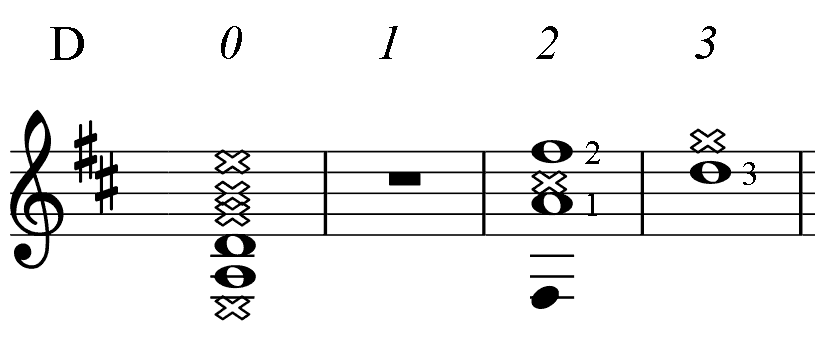
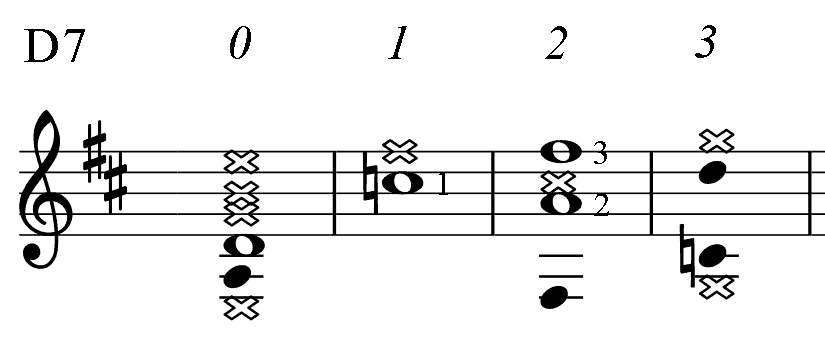
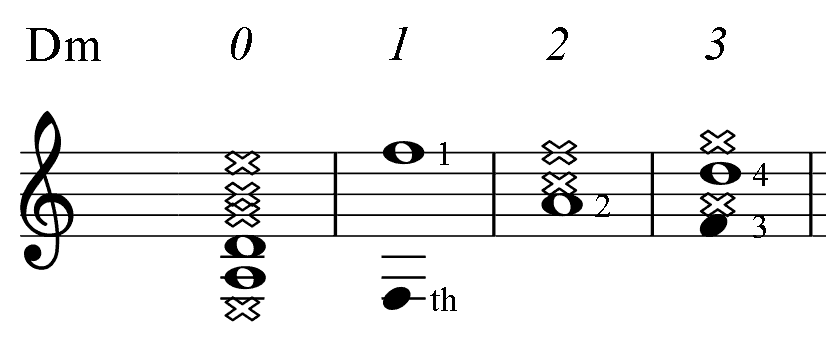
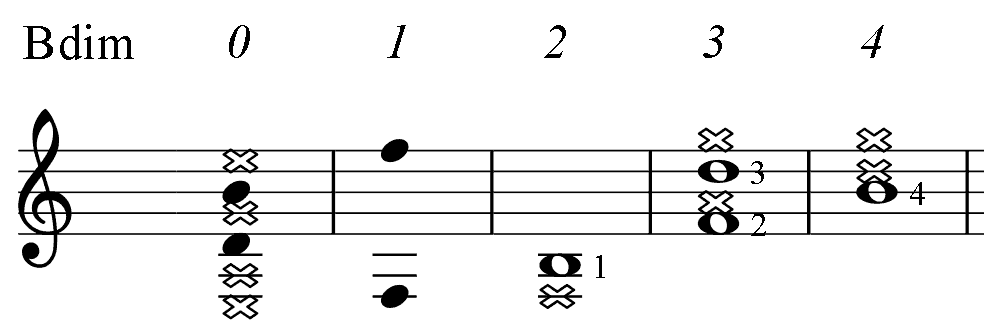
Below, for the reference, there are short diagrams of the most popular chord patterns given in several keys. This is the only table in the book where numbers indicate fingering. (For all other PAD diagrams, numbers near notes represent an order of the note in the mode: the root (1), 3-rd, 5-th.) Barre, if needed, is taken with finger 1. Chord notes are marked as whole notes. Notes marked dark are additional.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
08/28.2011
(from an earlier letter) "I think you'll be happy to know that this has accomplished more than you even set out for it to do. I'm no guitarist; I play piano (I've only been playing for around eight months, so I'm a beginner). I love how rich and full chords sound on guitar, but I was never really sure how to accomplish that same sound on a piano. I couldn't read guitar tabs, so every guitar site I visited was useless to me. Then I found your site, and it bridged that translation gap immediately. Thank you so much for creating this! " --
Patrick Hunter
Home | Top | What is PAD: Perfectly Aligning Diagrams | How the method was developed | Basic chord fingering chart | Table of PADs in the Book: chords and scales, transposition table | Musical structure of guitar starting with C major scale | Essential guitar scale pattern on the fretboard | Notes along the fingerboard: note C | Grouping of notes across the guitar strings into fret groups | Notes along the strings | Thirds intervals on the Guitar. Exercise | Guitar Triads and Tetrads (Chords), Diagonal Structure, Exercise | Chords and Inverted Chords on a Guitar Fret Group. Exercise | PAD Chord Charts | Working with other keys, C blues scale and A minor scale and key | Importance of Key Signatures | Guitar Ear, Fingering, Memory Training with Visual Musical Notes Presentation | The book | Success without memorizing | Blogs, Forums, Groups
| Available PAD in the key C - Am: | Help | Home | Explanation | Musical Structure of Guitar | Success without memorizing | Forums, Groups | ||
| Notes: | C, D, E, F, G, A, B | ||
| Triads of C major scale: | C, Dm, Em, F, G, Am, Bdim, tetrads: Bm7b5, G7 | ||
| Triads of A minor scale: | E, other: A | ||
| C blues scale | C7, F7, G7 | ||
| Chords over C major scale: | C, G, F, Em, Am, Dm, Bdim | ||
| Chords over A minor scale: | Am, Dm, E, G, C, F, Bdim | ||
| Donate $1 | Buy the Book | Order Custom | Facebook | Add to favorites | Mail to a Friend | Tweet | |
|
Key words: guitar, chord, scale, chart, classical, note, tablature, book, fingerboard, fretboard
Design and Copyright © 2011 Igor Polk. Published by Yes San Francisco, LLC on 2011.01.1