On Euclid's Theorem that
"In Isosceles Triangles the Angles at the Base are Equal"

This is the Euclid's Proposition 5 from Book 1

"Isosceles" essentially means "equally-sided" which is from latin which in turn is from greek is-o-skelos ( read like spanish ). It means "equally - legged". What do you think the first "isoskelos" figures would look like? Like a pyramid? The third side is called "a base".

1.

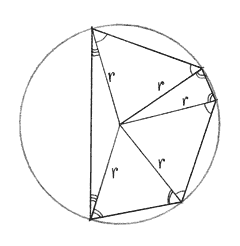
A usual depiction of an isosceles triangle like a pyramid or a letter A is a subjective choice. Any triangle build upon two radiuses of a circle or a sphere is an isosceles one and it can take any orientation in space.

2.

But we will use a usual drawing. Let ABC be an isosceles triangle where sides AB=AC. Need to proof that β equals γ.

Plan of the proof. So far we have one theorem on equality of triangles. It is Proposition 4 which says that two triangles are equal if two corresponding sides and an angle between them are equal. Therefore if we construct two triangles which are equal and ABC is a part of both of them and if β and γ are parts of them and have a certain symmetry we may be able to conclude that β equals γ.
3.

In his proof Euclid introduces an algebraic operation of difference on lines and angles. A "whole" may contain two parts and if there are two "wholes" and they are equal, and one part in each "whole" is equal", the reminding parts are equal. In other words:

Let for two systems 1 and 2

A1 = B1 + C1
A2 = B2 + C2

If A1=A2 = a, and B1=B2=b, it can be written:

a = b + C1
a = b + C2

From Euclid's "Common Notions" follows that C1 = C2

It works for line sections as well as for angles. And in the proof it is applied once to each.

4.

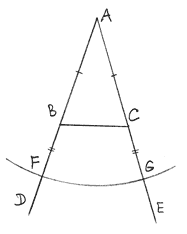Let's prolong the line AB (Euclid Postulate 2) and choose an arbitrary point F on it as it shown. A choice is made here, there could be another choice. Let prolong line AC and construct a point G such that AG=AF (Euclid Proposition 3). From 3 it follows that BF=CG. So, we did it for line sections.

5.

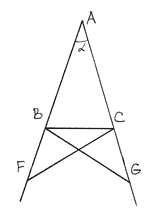
Let's construct lines BG and CF (Euclid Postulate 1). We have constructed triangles ABG and ACF.
Considering Euclid Proposition 4, AB=AC, AG=AF, and angle α is common. Therefore triangles ABG=ACF.

From here it follows that CF=BG and angles AFC=AGB. From 4, we know that BF=CG. Therefore triangles BCG=CBF by (Euclid Proposition 4 ).

6.

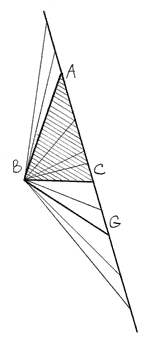A side note. ABC is a part of ABG. It is how to construct a triangle which includes an initial triangle as a part with prolongation of the side and taking a point on it outside of AC. Another case would be if a point G is taken inside AC. The drawing illustrates that a line a triangle side coinsides with is a place of points forming a family of triangles where each one is a part of another.

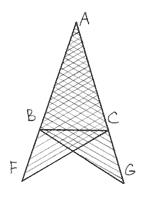According with the plan two triangles ACF and ABG are made and ABC is a part of each, it belongs to each.

7.

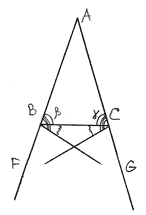Considering 3, from the construction, for angles:

ABG = CBG + ABC
ACF = BCF + ACB

and from 5, ABG=ACF, and CBG=BCG.

There fore ABC = ACB, or β = γ.
Q.E.D.

So we did 3. for angles

8.

From 5 follows that CBF = BCG, or "the angles under the base in isosceles triangles are equal".
Q.E.D.

9.

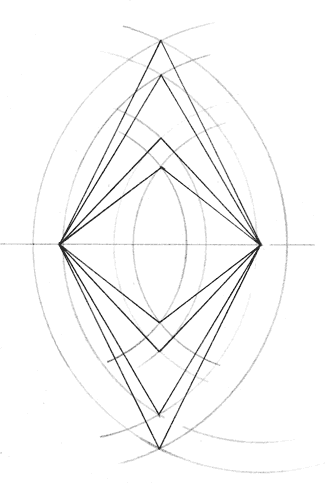Besides being formed by radiuses of a circle or a sphere ( see 1. ), isosceles triangle can be encountered, when two circles with the same radius intersect. A family of such circles drawn in the same plane around a pair of points and corresponding triangles is shown on the picture.

Problems

Problem 1

Prove that angles AFG and AGF equal.

Solution:

Triangle AFG is isosceles, there fore .. Q.E.D.

Problem 2

Construct an isosceles triangle ABC so that the base BC is parallel to the edge of the sheet of paper. You can use other theorems.

Problem 3*

Show (or prove) that it is impossible to prove that angles ABC=AFG based on first 5 theorems of Euclid. What is missed?